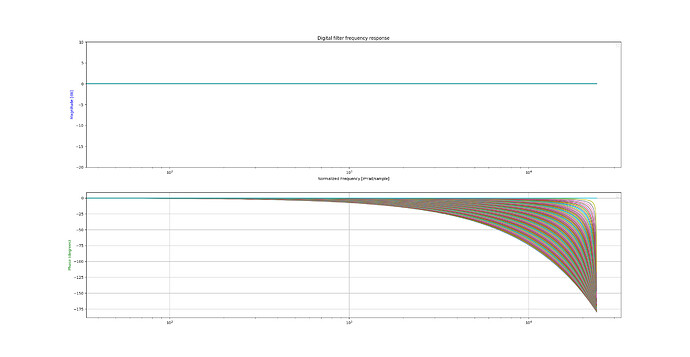
How to remove artifacts from all pass interpolation completely?

Development
1

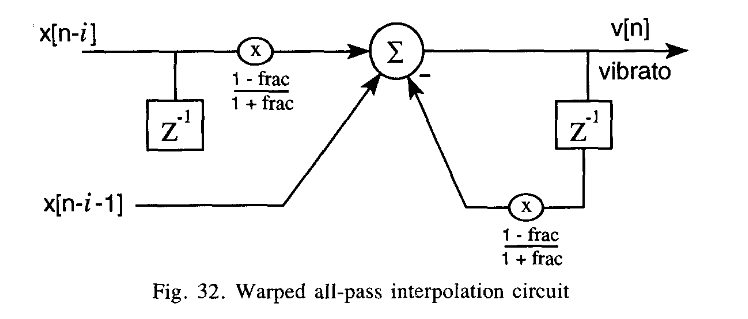
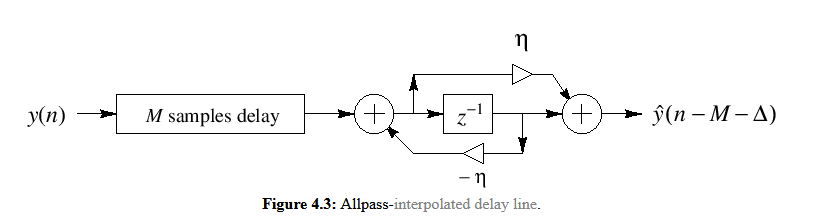
When working with fractional delay lines, all pass interpolation seems ideal because, unlike linear or hermite interpolation, it has no magnitude loss and only phase distortion. In my experience recently I have had much difficulty implementing all pass interpolation without clicks and pops on sustained sounds.

All Pass Interpolation Magnitude and Phase:

AllPassInterpolation
AllPassInterpolation2560×1327 239 KB

Dattorro discusses the use of all pass interpolation in-detail in his “Effect Design Part 2”. I won’t go into all the details, but more or less he proposes the following block diagram as a good option for an all pass interpolator:

image
image748×319 9.47 KB

This is more or less the same as the all pass interpolation method proposed on JOS’s CCRMA site.

image
image822×223 4.36 KB

I believe that, because all pass interpolation is recursive, it is very sensitive to changes in the coefficient “η” and large changes result in the clicks and pops. By keeping the coefficient value as close to zero as possible, we’re able to reduce the transient effect… aka limiting the fractional delay, frac, to 0.618 to 1.618 leads to the coefficient η having a value of -0.236 to 0.236. In practice, this works OK. The clicks and pops are definitely reduced using this exact method (see code below), but still evident on sustained sounds.

//Table size must be of size 2^N, where N is some integer
inline float InterpolateAllPass(float* table, float index, int32_t* size,
								float* delayBlock) {
	MAKE_INTEGRAL_FRACTIONAL(index)
	float xm   = table[(index_integral-1)&(*size-1)];
	float xmp1 = table[(index_integral)&(*size-1)];
	if(index_fractional < 0.618f) {
		index_fractional+=1.0f;
	}
	float f = (1-index_fractional)/(1+index_fractional);
	float v = xm + f*(xmp1 - *delayBlock);
	*delayBlock = v;
	return v;
}

Has anyone here successfully implemented an all pass interpolator that is artifact free? Upsampling by a factor of two or more reduces the artifacts greatly, but I can’t take this approach due to the CPU cost.

2

I implemented fractional delay lines using the techniques outlined in this paper “A Lossless, Click-Free, Pitchbend-able Delay Line Loop Interpolation Scheme”. Worked quite well.

3

Yeah I tried everything in section 2.2 of this paper (see code above). It reduced the clicks and pops but they’re still there on sustained sounds. The other sections: “2.3 The Legato Crossfade Trick” and “3 Glissable Allpass Interpolation” don’t seem relevant because I’m not doing legato/glissando. Unless you think otherwise?

Got a link to a module you used this on?

4

I used it in my VST plugin “Delay8”. Done years ago, not ported to VCV yet.

Delay8 uses modulated fractional delay lines. The modulation produces legato/glissando effects where the pitch changes (even slightly) as the read pointer position follows the modulation. For me, it was necessary to implement the features in section 2.3 and 3 to get a nice smooth all pass fractional delay line that was clickless with or without modulation.

1 Like
5

Cool! Thank you for the reply. I’ll give that paper another look. I tried a changing up a couple of things this week but still no luck. Even doing a simple modulated delay with all pass interpolation for a subtle vibrato effect gives me clicks and pops.

Is your VST still available online somewhere? I’d love to try it.

6

Isn’t every phase shifter a modulated all pass? I think they don’t inherently pop,like a generic biquad will.