The only thing missing is a way to modulate the harmonics levels.
I really don’t get the changes to the waveform adding harmonics introduces. Don’t need it explained, but it is even harder to get my head around the relationship between adding harmonics and the resulting waveforms.
One thing I stumbled on - that makes total sense once I think about it - you can turn off the root harmonic and transpose the incoming pitch by turning up other harmonics.
Your ears are very good in the frequency domain, your eyes are very good it the time domain. Mapping between the two of the in your head isn’t that easy. Which is a fancy way of saying “yeah, it’s not always obvious how the waveform relates to the individual harmonics”. If you spend a lot of time staring at waveforms and also at the Bogaudio Analyzer it might be fun, however.
For some values of ‘fun’ 
I went back and looked at the manual and solved one mystery, what happens when you pull down bars in the harmonics view - it changes the phase of harmonics. Actually possible to make some crazy waveforms.
Haha - it’s fun for me! Oh, and the Blamsoft wavetable module is a real treasure. Super good, and been around forever.
Well…without any explaining, it is difficult to transfer useful information.
I’ll just try to make some sense without making things to complicated (so I might cut some corners here and there).
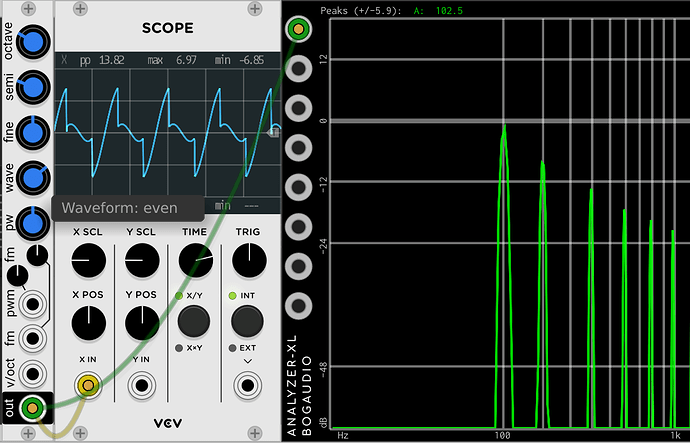
Let’s start by stating that several hundred years ago some french guy (Joseph Fourier) discovered that you can recreate any periodic function (waveform) by just summing enough sine waves (harmonics). He also delivered the math needed to “extract” the harmonics (their frequencies and amplitudes). The Fourier Transform.
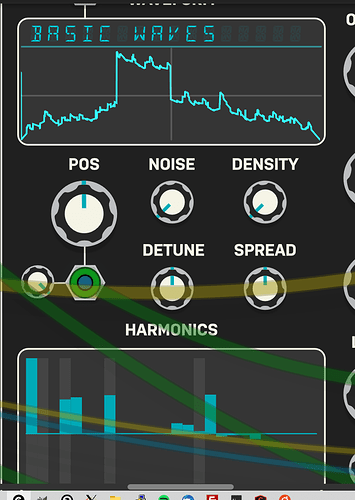
Each “bar” vertically represents the amplitude (“loudness”) of a single harmonic (a pure sine wave). The horizontal axis represents the frequencies. For a harmonic series, the first one is the root (“the note”). The others are multiples of the roots frequency (so 1x, 2x,3x,4x and so on). If you sum the sines, you get the waveform.
E.g. a saw has all harmonics with the ampitude 1 divided by its rank (so 1=1/1, 2=1/2, 3=1/3 and so on. Same for a square (50% pulse), but odds only (so 1=1/1, 3=1/3, 5=1/5 and so on). A triangle is like a square, but amplitudes ar 1/rank squared (so 1=1/1, 3=1/9, 5=1/25 and so on, sort of a low pass filtered square). Usefull info, since most synths will offer these basic shaped (though seldomly mathematically perfect).
So…since you can (re)create the waveform from these individual sines, it follows that if you change the amplitude any of these sines, the shape of the waveform will change. The other way around: if you change the waveshape, the sines needed to (re)create that waveform will also change (e.g. amount, frequencies and ampitudes). So…in general it’s a reversible transformation from time domain to frequency domain and vice versa.
Now I left out one more detail: the phase of each harmonic is also relevant. Usually the phases are represented below the horizontal line (and are often left out / static). Just changing the phase will also affect the resulting sum (waveform). Most of the time you can only shape/modulate the individual amplitudes. Sometimes phases as well.
So…if the shape of the waveform changes, it’s harmonic content (timbre/sound) will change. Same if you change the harmonic content directly, changing amplitude and/or phase of harmonics.
Synthesis priciples that manipulate waveshapes use this. Like waveshaping and amplitude, frequency or phase modulation. Generally this “deforming” will lead to non-lineair changes to the harmonic content.
Since additive synthesis (this summing of sines with their own frequencies and amplitude and modulation) is tedious work it never got to popular. A handfull of synths supported it as a main feature. Mainly in the digital domain. Like the Fairlight CMI and NE Synclavier (which even supported resynthesis) and the Kawai K5 / K5000 and the Kurzweil K150FS. But you can also via a Hammond Drawbar organ as an analog additive synthesizer implementation.
I wonder how many people will actually have ploughed through so many words and even read this last line.
I skipped to the end, so I read it, but it probably doesn’t count. I still have a K5, and programming sounds from scratch on it is still difficult.
As someone who has recently wanted to get my head around harmonics this is incredibly helpful - thanks for taking the time to write that all out!
I read it. I will probably need to read it a few more times.
I did. I actually know about Fourier transforms, dealt with them a bit doing brain imaging software. What I meant was that looking at the additive display, it isn’t clear to me how the harmonics change the waveform. What I do know is that shifting the phase changes the waveform in unexpected ways.
In in the XFX Wave, adding harmonics and shifting phase on a pure sine does what one might expect. But in the other wavetables, it seems to treat the current wave in the wavetable as a pure fundamental, and adding overtones gets messy fast, and shifting phases at the same time makes things get complicated timbrally quite fast.
I did 
Some of us love long form content you know. Great explanation! The XFX Wave is a fantastic module, I really hope it’ll be supported in V2. Made me wonder why the even harmonics waveform of the Befaco EvenVCO is not in more widespread use.
I think it adds that same wave in ratios of the harmonics to itself. So if you have a saw and add harmonic 1 and 2 it adds two more saws with 2x and 4x the frequency.
Me too. I cloned it for EV-3, or course. But perhaps unexpectedly it showed up in my Basic VCO as one of the waveform choices
Sort of. To get it exactly even (and ears probably can’t tell the difference) you take a sine at the fundamental, and then add a saw an octave up. And you need to mix them in exactly the right ratios.
I actually also still have a 1978 Kawai K5. It was pretty limited due to limited computing power. I remember it as having a NEC V30 as a CPU. A clone of ye olde IBM PC 8086 or 80286 CPU.
Low D/A samplerate. Low bitdepth (8 bit?) resolution. You hear slow envelope/LFO steps.
Still…it taught me a lot. And I spent many hours fiddling with its tiny buttons/datawheel and LCD screen. It does have a GUI (not just character based).
2 “DCO’s”, 64 harmonics (2x 64 or 1 x 128). Just 4 ENV per voice. Sort of Format filter (EQ). 16 voice polyphony, aftertouch. Pretty advanced state of the art in the late eighties.
Tech evolved…
Odds are just so simple to generate. A pulsewave is just periodically switching a signal with a fixed amplitude on and off.
Continuing the harmonics story…
Changing the pulsewidth will actually leave out each 1/pulsewidth harmonics. But looking at all of the amplitudes, they will look more like the combfilter effect. If you would draw a line over the amplitudes (sort like an env follower over the harmonics) it would look sort of like a “wave”.
Talking about combfilter effect: changing the phase of two waves will create a combfilter effect. Each of the harmonics within the spectrum will phase in or out (sum of phase and antiphade (180 degrees) = 0 (silence). But since the interval between harmonics is different, it has different effects all over the spectrum.
E.g. the interval between the first and second harmonic is a whole octave. But between second and third just half an octave. The intervals get ever smaller up the harmonic ranks.
Edit: Octaves in the harmonic series are at ranks 2^n, so 1, 2, 4, 8, 16, 32, 64 etc. There is no harmonic between the 1st and 2nd octave (ranks 1 & 2). There is only 1 between 2 & 4, there are 3 between 4 and 8 and ever more as you go up the octaves/ranks.
About the even harmonics. Since a Saw has all harmonics an 50% pulse only has odds, and both have amplitude 1/rank, you get even harmonics when you mix (sum) a saw and a phase inverted 50% pulse. The 50% pulses odds will cancel out the odds of the Saw.
Also, shapewise summing and phase shifting a Saw and a Ramp (a rising saw and a falling saw) will give you PWM emulation. Though you will also get an offset issue.
Edit: this is why several synths/oscillators will provide both Saw shapes, even though seperately they are interchangeable.
Again: note that “analog” waveshapes are generally not “perfect” shapes. In many (including the stock VCV) oscillators you get or can choose “digital” for mathematical perfect shapes. With these predictable harmonics.
Just some more basic info on exploiting shape, phase and harmonics.
Hope this is usefull/fun stuff you could add to your toolbox.
This is indeed the most simple approach to get even only. Multiply the frequencies of all harmonic of a Saw by 2. Which is simply detuning a Saw an octave up. It then has even only when compared to a Saw at the original frequency, an octave down.
It is literally relatively easy. (bad nerdy joke).
Yes, and of course just tuning a saw up and octave it will only sound like a saw an octave up. So something need to at least suggest the fundamental an octave down. which is why most VCOs that have an “even” output do this.
This shape is (of course) the result of both the amplitudes and phases of these even harmonics. I have not actually checked amplitudes and phases of an Even VCO like the one from Befaco.
