Don Cross / CosineKitty / Sapphire

Music & Patches
181

Typically a delay meant to be a tuned pitch source has a factional delay time, since delaying in even samples will be out of tune, especially at high frequencies. I’ve seen all kinds of ways of implementing this “fractional delay”. There’s lots written about it.

If sounds like you are trying to add feedback to a “normal” delay to generate pitches. As you note, this is pretty difficult!

btw, for any who care, the formula for frequency in Hz is f = fs / d, where fs is the sampling rate, d is the delay time.

182

:+1: thanks for the explanations, really helps to set out some of the hurdles involved.

183

Here is my creative fun for the evening, called Jungle Market. Dual Sapphire Echo chains create some fun rhythm interplay.

I used dual Venom VCO Units by @DaveVenom for the tonal voices, and Elastika and Hiss for percussive voices.

The patch is available here:

7 Likes
184

Tuning Tube Unit, they said it couldn’t be done!

Let me know if this is not the right topic for this.

Here I demonstrate the effect of Tube Unit tuning by first turning off Tube Unit and toning down other aspects of the patch. You notice that without Tube Unit’s resonances the synth sound is quite disharmonic. Second, I make the tuning really obvious by feeding Tube Unit noise instead of synth. Here you can hear the effect of tuned Tube Unit more subtly in context, but it’s still important for the patch.

You can use your ears or maybe a tuner to first tune all parameters and then find a magic ROOT input attenuverter position that would make the signal roughly correspond to V/Oct. It may or may not be 100% precise especially beyond 3 octaves or so, but then in a world where most use equal temperament no tuning is really precise anyway…

2 Likes
185

Very cool sounds! Tube Unit was one of those things where I had no idea how it would sound. I had to build it to find out! It is a weird critter that does what it does because that’s what it does. LOL.

2 Likes
186

In which Galaxy is again being a percussive instrument: link.

1 Like
187

I have been feeling a little creatively stuck the past few days. I kept feeling like, “I can’t think of anything original.”

Tonight I decided… OK, fine, I won’t be original. I’ll study work I admire and see if I can learn something from it. So I listened to a few tracks by Tangerine Dream. I wrote down some notes about elements of their style.

I decided to create a generative patch with the feeling of the Berlin School style of sequencer-driven synth. In honor of Tangerine Dream I call this track “Hypnocitrus”.

The patch is available here:

6 Likes
188

Today I was working on what I thought would be a 4-voice generative piece. I was especially enjoying the fourth voice, and I decided I wanted to play it manually. So I hooked up my MIDI keyboard and allowed 3 voices to play on their own while I improvised the fourth voice.

Here is the patch:

If you want to play the keyboard, select your midi instrument on the MIDI-CV module, then play only (or mostly) the following notes:

D#, E#, F, F#, G#, Bb, B.

[EDIT]: Oops! Corrected here, thanks to @Squinky:

C#, D#, F, F#, G#, Bb, B.

This will match what the 3 generative voices are playing. I’m just learning music theory, so this week I learned this is called either an Aeolian scale or a natural minor scale.

3 Likes
189

E sharp and f are the same note. E flat minor is e flat, f, g flat, a flat, b flat, c flat, and d flat. All the black keys.

190

The surge tuned delay modules may help? They even gave options to compensate for cable latency to stay in tune

191

I predict this comment will lead to 827 messages of which 84% contain the phrase actually or it depends……

1 Like
192

haha - i think you exaggerate, but yes, we may very well go into when e sharp and f are the same pitch and when they are not. I claim that unless one specifies otherwise, that one can assume 12 tone equal tempered tuning. Sure, I know there a zillion other tunings…

193

Theres two things. First tuning as you mention, but second the functional meaning.

In 12-TET E# and F are the same pitch, but they are not the same functional note. For instance, E# is the sharp third and F is the fourth in C. If you were writing in C and wanted a sharp 3 and sharp 4, you would want E# F# not F F#.

I just put this here not because you don’t know it but because I want to do my part towards getting to 827.

1 Like
194

Maybe temporarily do away with all musical formalities and get inspired by the complexities and delicate (im)balances of noise, clicks, filters, shapers and feedback loops?

E.g. from how my fellow Dutchman Thomas Ankersmit (ab)uses his Serge Modular…

[LIVE] THOMAS ANKERSMIT / SERGE MODULAR #6

195

Oops! Thanks for catching that. I typed in the wrong notes for D# Aeolian. I corrected my original post.

1 Like
196

Ooh, I feel like I can contribute some clarity to this conversation about music theory!

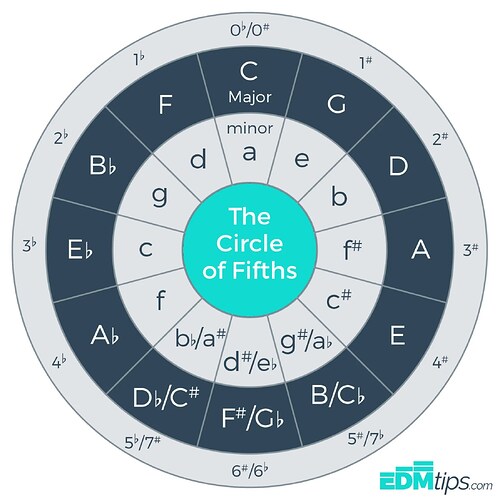
So firstly, when writing a scale, you pretty much always want to stick to only sharps or flats, here you have G# and Bb, which is what you would call a “diminished 3rd” since the letter names G and B are a “third” apart, and that third is diminished in quality (a minor third is always 3 half steps apart from the other note, diminished is one less) what you see happens is that you now have one letter name missing (actually 2, as there is one missing previously as well), and a duplicate letter name. The idea with conventional modal scales like this with 7 notes is that we want to keep all the letter names in the scale without any duplicates or omissions. If you mix sharps and flats, you’ll typically run into this issue precisely because of the thing that has happened here. It doesn’t matter so much when writing out the letter names, but on sheet music, this would look very clearly wrong. (not to imply that you need sheet music or something, just that it would make this a little more obvious)

Secondly, on the subject of E#s, B#s, Cbs, and Fbs. They are real notes in the sense that they are actually used outside of a theoretical sense. Its only that certain scales, as you “add” accidentals to the key and scale, in order to maintain the order of note names as I was mentioning earlier, they are required to remain within the key. So take for example C# major (or Ionian, if you prefer modes), the letter names would be C#, D#, E#, F#, G#, A#, B#. They could be described as “the same note”, but as @Squinky mentioned, they are typically to serve a different descriptive purpose.

As for the scale you have, I think you might have meant to write E instead of F for the third note, because this scale is major in quality. I don’t remember what this particular scale would be called off the top of my head (ionian dominant perhaps? Been a while since I’ve encountered altered modes). Anyways, the full correct scale for C# Aeolean should be C#, D#, E, F#, G#, A#, B

2 Likes
197

Just noticed this as well. in D# the scale would be D#, E#, F#, G#, A#, B, C#. You could also reasonably write this in flats, since you would have the same thing with a weird altered white note. Eb, F, Gb, Ab, Bb, Cb, Db. Pick your poison!

198

Yeah, I just screwed up typing the notes in the scale and didn’t notice it! Thanks to Squinky for catching it. I corrected my original comment with strike-through of the mistake.

199

Yes. I was thinking about this today. Of course this may only apply to “traditional” scales and modes. One practical reason for this is that it would be impossible/difficult to notate a key signature otherwise. Which is sort of why e flat minor is called that, instead of d sharp minor.

200

Yup! really only applies to 7 note scales that fit on a staff. You can pretty much ditch it if you are doing any alternate tuning scales, or scales with more than 7 notes.

Your relation to key signatures is correct. This is really what the circle of fifths is showing. When you move your root note of a scale by a fifth (or fourth to go the other direction on the circle), you add or subtract exactly one accidental. If we mix sharps and flats, this entirely breaks down the key signature. When you start getting into keys with lots of sharps and flats, you get to a point where switching accidentals makes more sense than going into double accidentals, but eb minor and d# minor sit at the point where both have an altered white note, so either one is acceptable, but most instrumentalists (as in wind and brass players usually) prefer flats because their intsrument is naturally tuned to them.

The-Circle-of-Fifths_-EMDtips.com-1-726571236
The-Circle-of-Fifths_-EMDtips.com-1-7265712361701×1701 202 KB

as you can see, d# sits at the very bottom of the circle, right at the crossover of sharps and flats. You technically can add one more sharp without resorting to double sharps (shown as a# minor, adding the accidental B#, the only other possible accidental sharp white note), but at that point the flat key signature has less accidentals, so why not just use that!

1 Like